物理科学研究部

 こんにちは。物理科学研究部です。物理科学研究部では宇宙物理学系、物性物理学系、基礎実験系、数学系の４分野に分かれ、自分たちで物理学などの自然科学の問題を見つけ、研究する活動を行っています。各分野には班があり、宇宙物理学系にはシミュレーション天文学班と観測天文学班、物性物理学系には物性実験班と物性理論班、基礎実験系には基礎実験班、数学系には数学班が存在します。本記事ではそれらの班の内、シミュレーション天文学班、観測天文学班、基礎実験班、数学班が自分たちの研究に関係するトピックや研究活動について簡単にご紹介したいと思います。お楽しみ頂ければ幸いです。

 

シミュレーション天文学班

主な活動

主に、自身で提起した問題をシミュレーション等を用いて理解、及び解決していくという活動を行っている。

学年に応じた流れ

1年 プログラミングの基礎を自身で学習する。シミュレーション天文班では、例年C言語の内容を扱っている。自分でポスター作成、報告書作成をして自分の研究内容を発表するという研究の簡単な流れを体験する。


2年 自分の課題に沿った研究を進める。必要であれば自習して足りない知識を補いながらプログラムをしていく。1年生のサポートを主に行う。


3年 やることはほぼ2年生と同様。院試もしくは就職を見据えて各々が勉強している様子。

 

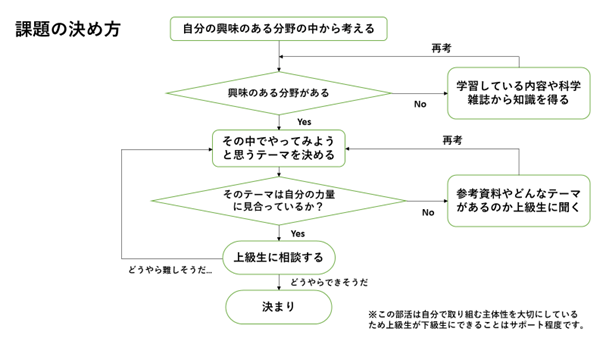
研究課題の決め方

 

主に以下のフローチャートのような順序で自分の研究課題を決めていく。

研究で扱うトピックの解説

 

スイングバイ

 天体の引力を使用して探査機の航路を変更する技術のこと。燃料を節約することができる。

 

コリオリ力

 メリーゴーランドのような回転する座標系において移動した物体が受ける見かけの力の一種

 

重力波

 ブラックホールや白色矮星が時間変動する重力で時空を歪めるときに発生する光速で伝わる波のこと。

 

まとめ

 

天体のシミュレーションに興味がある人はぜひ来てください。お待ちしております。

もちろん物理科学研究部自体に興味がある人もお構いなく～。

 

 

 

観測天文学班

紹介

観測天文学班は、現在3年生1人、２年生1人で活動を行っています。観測天文学班では、観測データから研究することを主としています。

研究

実際の活動として、観測データの解析や、道具の作成をしてきました。データの解析では、既存のデータをALMAから取得したり、実際に天文台などに行き観測をしてデータを取得します。そこで、データの解析を行い、星や銀河の組成、温度、距離、速度などを調べることができます。道具の作成では、望遠鏡、分光器の作成を行いました。実際に、作成した道具で観測を行い、道具の評価を行います。

問題

  1. 宇宙マイクロ背景放射（CMB）とは？
  2. ダークマター（暗黒物質）とは？

解答は一番下


 ←実際に観測した月

 

  1. 宇宙の色々な方向から、一様に降り注いでいる電磁波。CMBは、ビッグバンの直後に発生したと考えられており、これを観測することで初期の宇宙を知ることができる。
  2. 宇宙に存在する物質の約85％を占めるといわれている謎の物質。そして、ダークマターは光学的に直接観測することができない。しかし、間接的に存在をしめす観測事実が増えている。

 

 

基礎実験班

 

　基礎実験班では個々人の興味関心に応じて、物理学などの分野での基礎的な実験を行いその考察をしています。本記事では馴染み深い円周率の様々な求め方を簡単に紹介します。

 

円周率πを求めよう

π=3.14159265358979323846264338327…

 

算数や数学でお世話になる円周率ですが具体的にどのような方法で値を求めているか知っていますか？

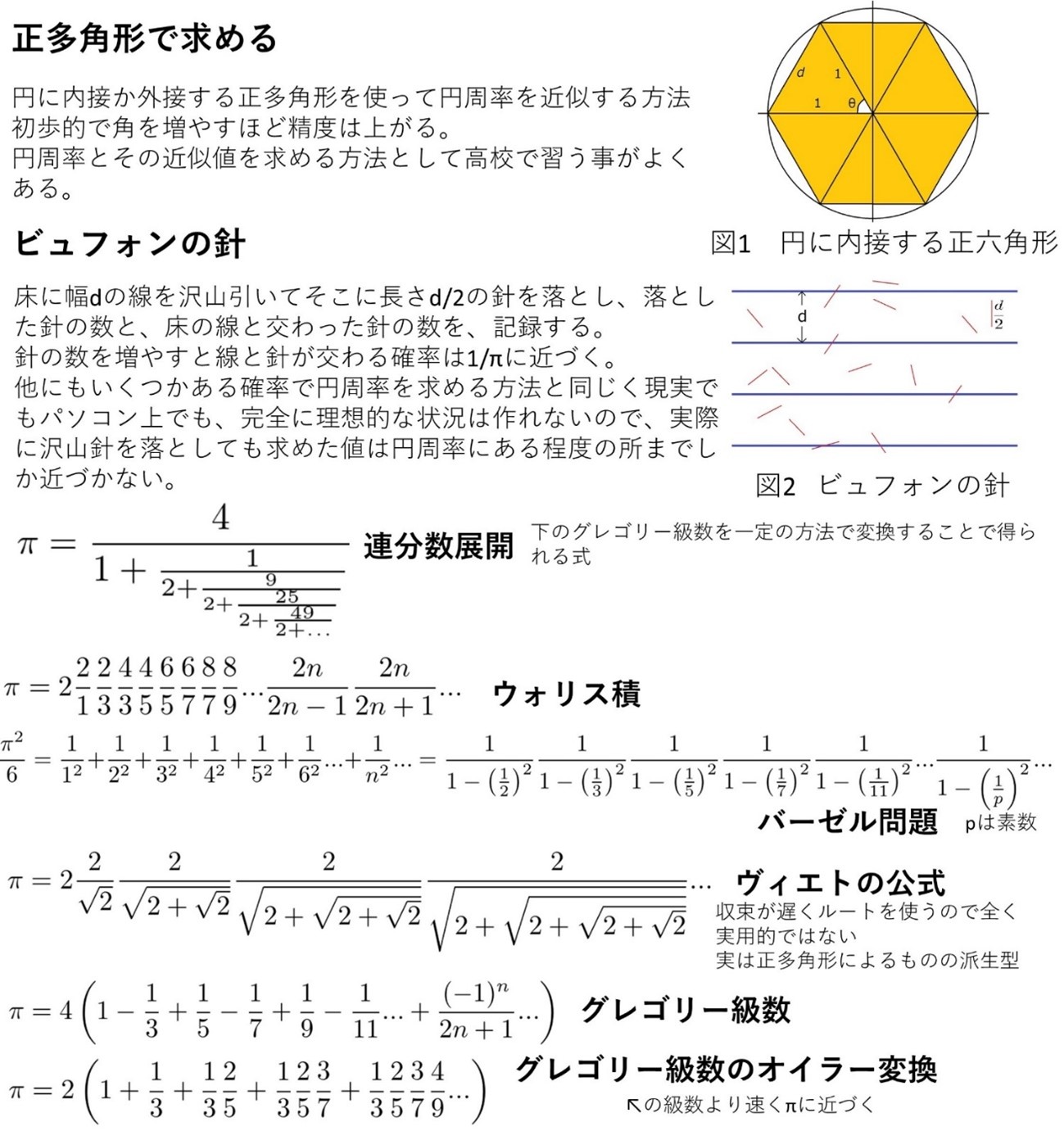
円周率は図形の円以外でも様々なところに出現するので昔から研究されており、いろいろな方法で求めることができるのが知られています。ここではそういった数式などを紹介します。

簡単な紹介なので証明は載せませんが大半は高校レベルの知識で理解できるものなので興味が出たら調べてみると面白いですよ。

参考文献

蟹江 幸博, 有理数と無理数のはざま-連分数について-, p 13, “http://kanielabo.org/papers/kanagawa.pdf#search='%E9%80%A3%E5%88%86%E6%95%B0%E5%B1%95%E9%96%8B+%CF%80'”, (参照 2020-9-14)

遠野 節夫, 石村 隆一, 野田 健夫, 安冨 真一, 山方 竜二, 理科系の基礎 微分積分, p 79(2018)

Michael J. de Smith, Maths for the Mystified: An Exploration of the History of Mathematics and Its Relationship to Modern-day Science and Computing, p 165(2006)

  1. Yaglom, I. M. Yaglom, An elementary derivation of the formulas of Wallis, Leibnitz and Euler for the numberπ, p 181(1953)

” http://www.mathnet.ru/links/4088c8ca179a38de2ee7837305ce50a3/rm8256.pdf”, (参照 2020-9-14)

啓林館, 未来へひろがる 数学2, p 151(2012)

中村 亮一, ニッセイ基礎研究所 円周率πが現われる世界－ビュフォンの針の問題－(2017), “https://www.nli-research.co.jp/report/detail/id=56991?site=nli”, (参照 2020-9-14)

大浦 拓哉, 円周率の公式と計算法, “http://www.kurims.kyoto-u.ac.jp/~ooura/pi04.pdf#search='%E5%86%86%E5%91%A8%E7%8E%87+%E3%82%AA%E3%82%A4%E3%83%A9%E3%83%BC%E5%A4%89%E6%8F%9B'”, (参照 2020-9-14)

 

数学班

こんにちは。物理科学研究部数学班です。数学班は今年設立された班であり、主に純粋数学の問題について研究しています。今後はゲーム制作や囲碁AIの作成などの情報科学にも活動領域を広げていきたいと考えています。本記事では大学で学ぶ数学の世界の一端をご紹介できたらと思います。

 

  • 1+1=0が成り立つ！？不思議な有限体の世界

１＋１＝２という数式は小学校から馴染みのある式の一つであるかと思います。２＋３＝５、６＋７＝１３も同様に。しかしながら、こうした簡単な数式が成り立たない世界が、大学での数学にはあるのです。それは「有限体」と呼ばれる世界で、高校生の方なら知らず知らずの内に同様の世界を見ているのではないでしょうか。

　有限体の紹介をする前に、少し自然数と整数、体と呼ばれる数学的対象についてご紹介したいと思います。

　自然数とは皆さんご存じのとおり、１、２、３、…と続く数のことです。もう少し大学数学っぽく書くと

 

ℕ＝｛1,2,3,…｝

 

となります。また整数は

 

ℤ＝｛0,±１,±２, …｝

 

となります。この様に数や図形、文字などをより集めて括弧で括ったものを集合といい、その中にある数や図形を要素や元といいます。上の書き方では自然数の集合は｛1,2,3…｝であり、その要素は1,2,3…という個々の数です。こうした集合の上で、足し算や掛け算といった計算（演算）が可能である集合のことを群とか環とか体と呼びます。非常にざっくりとしたイメージとしては、群はただ一つの演算（例えば足し算（とその逆の引き算）のみ）、環は２つの演算（例えば足し算と掛け算）、体は四則演算（加減乗除）が成り立つ集合として捉えて頂ければ、本記事の範囲では問題ないと思います。整数は足し算（とその逆の引き算）が成り立つので、群になります。一方、自然数は足し算＋が成り立つ（自然数２つを足した結果も自然数になる）のですが、その逆演算である引き算が成り立たないので群にはなりません。（集合が群や環になるにはある演算の逆演算ができることが要請されます。）馴染みのある実数は加減乗除が可能であるため、体となります。そして、有限体はその名の通り体になります。

　では、有限体とはどんな集合なのでしょうか。有限体とはざっくり言うと要素の個数が有限個の体のことです（その名の通りですね）。これがどうして１＋１＝０のような不思議な現象を持つのでしょうか。それは異なるものを同じものとみなす「＝」の意味に秘密があるのです。異なるものを同じものとみなすことにより数学の世界は広大に広がっていきます。

　有限体で生じる現象と同様の結果が得られるものが高校数学にはあります。それは「あまり」をみる計算（modの下での計算）です。modは法とも呼ばれ、8≡1(mod 7)のようにmodの数で割ったあまりが等しい数を同じものとみなす演算のことです（法の下で異なる数が平等とみなされるのですね）。お気づきの通り、先ほどの８と１以外にも、29≡15≡8≡1(mod 7)と同じ数は無数にあります。では、mod２の時はどうでしょうか。このとき、2≡1+1≡０(mod 2)が成り立ちます。つまり、1+1≡０が成り立ちます。自然数では１＋１＝２となるのでした。

　有限体でもmodを用いた計算と同様の計算が成り立ちます。しかし、有限体においてmodの役割をする数は標数と呼ばれ、任意の数でなく素数ｐになります。（これは定理として成立します）。有限体Fpは集合として以下のように表せます。

Fp={0,1,2,…,p-1}

 

そしてFpの任意の２元a,bに対し、足し算＋が成り立ち、掛け算×も成り立ちます（mod pにおいての足し算と掛け算を見て頂ければわかるかと思います）。また足し算の逆演算である引き算―と除算÷も成り立ちます（より厳密にいえば、引き算はFpの元aと0に対して、a+(-a)=0となる元-aとFpの元bとの足し算、除算はFpの元aと１に対して、a×a^{-1}=1となる元a^{-1}とFpの元cとの掛け算として扱われます）。除算は少し工夫が必要ですが、例えば６÷４は6÷４＝XとなるXについて、６＝４×Xを得るというのが有限体における除算になります（つまりはa^{-1}を求めます）。例えばp=７ならば６＝4×5でX=５となります。このように足し算、引き算、掛け算、割り算の四則演算が成り立つため、有限体は体となります（本来ならもっと厳密な論証が必要なのですが、代数構造としての雰囲気としてはこの方が想像しやすいかと思います）。ｍod　pによって同じと見做される数をまとめ上げたものを有限体として捉えても良いかと思います。有限体がmodを用いた計算と異なる点としては、演算が入った集合として成立している（つまりは群や環の仲間である体）ということです。これにより、他の群や環、体との関係を考えることができ、modのみでは見えなかったより広い世界を見ることができるようになるのです。

　最初の話題に戻すと、1+1=0となるのはp=2である有限体Fpの場合です。特に、この場合において成り立つ現象として、零関数と零多項式は異なるもの、というのがあります。零関数とは、をある集合Aの元として、関数は常に０を返すものを零関数といいます。零多項式とは多項式(a_n)(x^n)+…+(a_1)x+a_0について(a_n)(x^n)+…+(a_1)x+a_0=0となるような多項式の係数a_n,…,a_0が全て0であるものです。零多項式ならば零関数は自明です。しかし、零関数ならば零多項式は常には成り立ちません。有限体F2の元をxとして、多項式x(x-1)=0は零関数ですが零多項式ではありません。そのため、零関数は常に零多項式とは限りません（が属する集合と多項式の係数が無限体ならば成り立ちます）。このようにして、modを用いた場合とは違って有限体はmodの演算とそれにより同じとみなされる数達を集合として扱えるため、有限体によって見えない世界が見えないようになります（有限体の世界は本当に広く、今なお研究され続けています）。そこが、modという計算内容に注目するものか、有限体というmodの計算を内包した集合として考えることの違いかと思います（有限体で行われる計算はmodの計算と本質的には同じでしょうが、代数という枠組みにすることで扱える幅が広がっていると考えます）。このようにして、有限体はmodを元にして一つの体を持って立ち上がるのでした。

　modを元にし、有限体という体を持った数学的構造物になることで、零関数と零多項式は異なることがあるという事実を得るのでした。そして、F2では小学校から馴染みの深かった1+1=2という式が成り立たないのでした。これはmodという異なるものを同じものとみなす方法によって得られたのです。

このようにして、異なるものを同じと見ることで見える世界ががらっと変わって見えることがあります。そのようにして世界を見ることで、今まで同じだと思ってみていたものが違って見えたり、違ったものが同じに見えるという発見があるのではないでしょうか。そしてそうした発見は数学を学ぶ喜びであり、人生をも豊かにするものと考えます。そのような発見の一端に本記事がなれたなら、望外の喜びです。

 

 

参考文献

　[1]　D.コックス、Jリトル、Dオシ―（著）、落合啓之、示野信一、西山享、室政和、山本敦子（訳）『グレブナ基底と代数多様体入門　（上）』　Springer　 2000年

　[2] 松坂和夫『代数系入門』　岩波書店　2018年

 

 

　以上が物理科学研究部の紹介記事となります。通常の学校祭ならばポスター発表を行い私たちの研究を皆さんに直接ご紹介できるのですが、今年度はこのような形式での発表となりました。来年こそは皆さんに直接研究を紹介できることを願い、その日が来ることを楽しみにしています。

一覧に戻る